Mengubah Derajat ke Radian, dan Radian ke Derajat

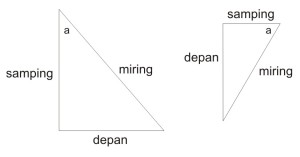
Sudut itu satuannya derajat. Sedangkan bilangan di dalam kehidupan sehari-hari kita berada di bilangan real. Bagaimana cara mengubah satuan derajat ke dalam bilangan real?

Pada mata pelajaran trigonometri, kita perlu sudut. Misalnya sin(30). Tentunya 30 tersebut di dalam satuan derajat. Tetapi bagaimana cara kita untuk menggambarnya di dalam koordinat cartesius.

Padahal di dalam koordinat cartecius itu sendiri merupakan bilangan real. Misalnya kita akan menggambarkan grafik dari sin(x). tentunya derajat tidak sama dengan bilangan real. Yang akan kita berikan sekarang adalah bagaimana cara mengubah derajat ke dalam bilangan real.

Perbandingan trigonometri pada segitiga siku-siku

Tulisan kali ini membahas tentang perbandingan trigonometri pada segitiga siku-siku dan cara mudah menghafal perbandingan tersebut.

Dua gambar tersebut adalah segitiga siku-siku. Dan salah satu sudutnya kita namakan sudut a. segitiga siku-siku mempunyai tiga sisi. Dan kita akan menamainya dengan sisi miring, depan dan samping.

Sisi miring yaitu sisi yang terletak di depan sudut 90 derajat. Sisi depan adalah sisi di depan sudut (untuk gambar tersebut, terletak di depan sudut a). sisi samping adalah sisi yang terletak di samping sudut a.

Grafik fungsi trigonometri dan periode

Berikut ini adalah 3 gambar grafik trigonometri yang mendasar, yaitu grafik fungsi sinus, grafik fungsi kosinus dan grafik fungsi tangen. Untuk grafik fungsi trigonometri yang lainnya, bisa digambar di software grafik yang pembaca miliki.

Cosinus

Nilai trigonometri sudut lebih dari 90 derajat

sinus	0				1
cosinus	1				0
tangen	0		1		-

Tentunya sebagian sudah hafal dengan tabel tersebut. yaitu nilai trigonometri untuk sudut-sudut khusus dari 0 derajat sampai 90 derajat. Nilai-nilai tersebut diharapkan untuk dihafal. Menghafalkannya cukup mudah, teknik menghafalnya juga banyak, salah satunya yaitu : “Setengah akar …”

Untuk sinus.  nilainya berturut turut . Jika disederhanakan menjadi :

Lingkaran

Siapa yang tidak mengenal lingkaran. Anak SD pun tahu apa itu lingkaran. Di sini akan kami bahas mengenai lingkaran. Tentunya masih dasar-dasarnya saja. Lebih khusus lagi yaitu untuk anak SMP kelas 8. Semoga lebih mudah untuk dipelajari.

Unsur-unsur pada lingkaran yang wajib diketahui.

Jari-jari

Sangat mendasar. Pada gambar, jari-jarinya adalah garis OB, atau garis OC atau OA. Jari-jari adalah jarak dari pusat lingkaran

Diameter

Adalah garis lurus yang melalui pusat lingkaran dan menghubungkan titik pada lingkaran dengan titik yang lain pada lingkaran.

Garis Singgung Dua Lingkaran

Garis singgung dua lingkaran. Sebelum membagi kasusnya, kita perhatikan beberapa hal penting mengenai bab kali ini (garis singgung lingkaran). Pokok pentingnya sebagai berikut :

Notasi Ilmiah

Notasi Ilmiah atau bentuk baku ini digunakan untuk menuliskan bilangan yang sangat besar. atau bilangan yang sangat dekat dengan nol. Tepatnya yaitu diantara 0 dan 1 atau diantara 0 dan –1. Tujuannya yaitu agar penulisan angka tersebut lebih ringkas. Bagaimana kita mau menuliskan angka yang sangat panjang. misalnya 1230000000000 dan 0.0000000827.

Penulisan notasi ilmiah atau bentuk baku ini dilambangkan dengan a x 10ⁿ. dengan a lebih besar atau sama dengan 1 dan kurang dari 10.  Dan n adalah bilangan bulat. Semua bilangan real bisa dituliskan dalam bentuk baku. Misalnya saja angka 2. Jika kita tuliskan ke dalam bentuk baku menjadi 2 x 10⁰. Karena 10⁰ = 1, maka 2 x 1 = 2.